Technical Note No. 98/6 - Task 4/1 (Wave Spectrum) Explained
Each burst pressure time series is converted to a time series of hydrostatic depth and the power spectrum of the hydrostatic-depth time series is computed and stored.
DOBIE calculates hydrostatic depth from pressure as:
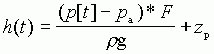
where h(t) is the water depth time series in metres, p(t) is total pressure time series in pounds per square inch sensed by DOBIE, zp is elevation of DOBIE above the bed, g is acceleration due to gravity (9.81 m/s2), r is water density and F is a factor (6895 kg/[s2m]/psi) used to convert pressure in pounds per square inch to pressure in kg/(s2m). For this calculation, DOBIE assumes the water density to be 1025 kg/m3 (which is a typical seawater density) and the subtraction of 10 m is a correction that removes a depth of water equal to a nominal atmospheric pressure. h(t), as defined, will only equal time series of "true water depth" (i.e. sea-surface elevation around MSL plus mean water depth) when there are no waves present, because the conversion from pressure to depth as stated does not account for the fluctuating component of pressure due to waves. The average of h(t), which is reported by the PEDP,is the true mean water depth (see Technical Notes 98/3 and 98/4).
The number of spectral estimates, NS, is given by:
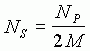
where NP is the number of points per burst and M is the merge. The greater the merge, the smoother the spectrum and the fewer spectral estimates.
The first spectral estimate is at the frequency:
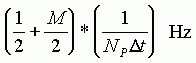
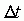
where is the sample interval in seconds. Note that frequency is the reciprocal of period; it is not radian frequency.
The frequency-interval between spectral estimates is:
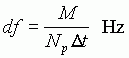
The greater the merge, the coarser the resolution of the spectrum.
The integral of the power spectrum over all frequencies is equal to the variance of h(t) (there is no 2p involved). That is:
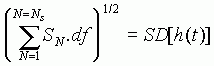
where SN is the Nth spectral estimate.
MOG June, 1998
